EM Radiation

As Chemists we often generalize all electromagnetic radiation as "light".  While often we are talking about visible light, we can also lump in UV or infrared radiation or even x-rays or radio waves.  All of these are electromagnetic radiation: a traveling wave characterized by an oscillating electric and magnetic fields.

These waves are characterized by three inter-related parameters: wavelength, frequency, and speed. Since the speed of light in a vacuum is a constant, wavelength and frequency end up as two different ways to convey the same information. Therefore EM radiation can be either described by its wavelength or by its frequency but these are completely interchangeable.

Wavelength

The wavelength of a light wave (or any other wave) is the distance between two peaks of the wave.  As it is a physical distance, it has units of length. It is hard to "visualize" light as having a physical wavelength, but it does. That is not to say you can hold a ruler up to it and see how far it is between peaks and valleys. But, it does mean that this will have many implications for how a chemist might try to use light in an experiment. For example, a key characteristic of waves is diffraction. This occurs when the wave interacts with a group of objects that are separated by a spacing that is similar to the wavelength. Many compounds have atoms that are separated by distances of 0.1 nm. Therefore we would expect they would diffract light with similar wavelengths. X-rays have these wavelengths and are regularly used by chemists to determine the distance between atoms in a compound with x-ray diffraction.

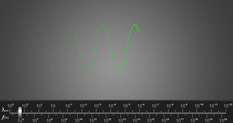
Below is a picture of a wave denoting the wavelength with the symbol we commonly use a Greek lower case lambda, λ.

Speed of Light

The speed of light in a vacuum is another Universal constant. We say that the speed of light is constant not because it is always the same, but because the speed of light in a vacuum is the same for all types of light. The speed of light actually varies (slightly) depending on the medium that it is traveling through. However, for all of our problems, we will consider the speed of light to be the speed in vacuum. This value is the same for all frequencies and is

\[c = 2.998 \times 10^8 {\rm m\;s^{-1}} \]

Note: This is really, really fast. As such in our everyday experience, light travels from place to place essentially instantaneously. Nevertheless, the speed of light is critical for our understanding as we use it to relate wavelength and frequency.

Frequency

The frequency of light is the number of peaks that pass by a given point in space per second. For all waves, this depends on both the speed and the wavelength. The relationship for light is

\[c = \lambda \nu \]

where c is the speed of light, \(\lambda\) is the wavelength and \(\nu\) is the frequency. Since speed has units of distant per time, and wavelength has units of distance, frequency has units of inverse time. We will use units of inverse seconds which are typically called Hertz, abbreviated as Hz.

The small simulator below graphically shows the relationship between the frequency and the wavelength (note: it is not to scale as the wavelengths are changing over many orders of magnitude).

click to view

Types of Radiation

We can classify different types of "light" or electromagnetic radiation by their wavelengths (or frequency).

We typical use 7 categories ranging from the shortest wavelength to the longest.

In order from shortest to longest wavelength we have:

Gamma Rays
X-Rays
Ultraviolet Radiation
Visible Light
Infrared Radiation
Microwaves
Radio waves

Note: they are all radiation and they are all waves (and they are all "light"), but we typically use different names for different categories.

The Visible Region: It is worth memorizing some of the details of the visible region - it serves as a "marker" region for the other regions. Even though the colors of the visible spectrum fade off into the "invisible" ultra-violet and infra-red regions we generally say that the visible spectrum is located between 400 nm and 700 nm. It is also handy to remember the order of color in the visible region. The easiest (and oldest) is to remember "Roy G. Biv". That will help you remember the order of colors of the visible spectrum (or of the rainbow if you prefer). Don't worry about specific wavelengths other than knowing that 400 nm is the "blue" end of the spectrum and 700 nm is the "red" end. The visible spectrum show below:

The diagram below (from Wikipedia) shows all of the regions within the electromagnetic spectrum. They try to give you a nice real world object to compare the wavelength to. You can (and should) read more at the Wikipedia website: //en.wikipedia.org/wiki/Electromagnetic_spectrum

Photons

The energy of light is different than energies we are used to dealing with in our everyday world. This is because we can think of the energy of light as being packaged up into small pieces with a particular energy. These "pieces" are not really little pieces or particles it is just easy to think of them that way because of the way they interact with things such as electrons. The energy of these photons is proportional to the frequency of the light, and the proportionality constant is called Planck's constant. Thus, the energy is given by

\[E_{\rm{photon}}=h \nu\]

where E is the energy, \(\nu\) is the frequency and h is Planck's constant. It is useful to note that Planck's constant is an incredibly small number

\[h= 6.626 \times 10^{-34} {\rm J\;s}\]

So even very high frequency EM radiation like x-rays have photons that are tiny amounts of energy. However, everything is relative and tiny to you and me can be enormous relative to the energy of an electron.

Why do we think of the energy as being packaged like this? Because we find that for interactions of light and electrons that the interactions are one photon for each electron.

So if we have bigger and brighter light sources, they have more total energy, but the energy per photon is only determined by the frequency. And the energy per photon is the only value that matters for the electron.

Photoelectric Effect

The photoelectric effect was key to the development of the idea of a "photon" or the relationship of the energy of light to its frequency. The photoelectric effect is simply the effect that sometimes when you shine light on a metal, electrons are ejected. There are several key findings that we investigated in class.

1.  Unless light of sufficient frequency is used, then no electrons are ejected. That is there is a threshold below which no matter how intense the light source is, no electrons leave the metal.

2.  If you are using light of a sufficient frequency, then as the light source is increased in intensity (brightness), the number of electrons ejected increases.

3.  As the frequency is increased above the threshold, the velocity of the ejected electrons increases.

From this we can conclude that energy is proportional to frequency and that the proportionality constant is Planck's constant.

\[E=h\nu\]

Planck's Constant, \(h= 6.626 \times 10^{-34} {\rm J\;s}\).

We can also examine the relationship between the kinetic energy (\(E_{\rm k}\)) of the electron and the frequency of the light used in the experiment. The maximum kinetic energy of the electron is the energy of the photon minus the threshold energy. This threshold energy we call the "work function" and we give it the symbol \(\Phi\).

\[ E_{\rm k} = {1 \over 2}mv^2 = h\nu - \Phi\]

So we can either predict the maximum velocity of the electron for a given frequency if we know the work function or by measuring the maximum velocity for a given frequency we can calculate the work function.

Another way to think about this is simply conservation of energy. The energy of the photon must equal the sum of the work function (the potential energy that needs to be overcome for the electron to "escape") plus the kinetic energy of the electron. This is the same as the above equation re-arranged.

\[ h\nu = E_{\rm k} + \Phi = {1 \over 2}mv^2 + \Phi\]