The great diversity of properties of different materials arises from the multitude of different compounds that can be formed. Compounds are materials that are composed for multielements. To understand how these different compounds form requires and understanding of chemical bonding. Chemical bonding refers to the simple idea that a collection of atoms may have a lower energy when they are in close proximity to each other than when they are separated. Because these atoms stay in this lower energy configuration the appear "stuck" or bonded to each other.

We generally divide types of bonding into two limits: Ionic Bonding and Covalent Bonding. It is important to note that these are two extreme models of chemical bonding and many compounds have bonds that might be best described as some combination of both. However, we can understand a great deal by simply considering the two extreme cases.

This first video is a big picture view of why chemists are interested in the idea of "bonding"

Ionic Compounds

Ionic compounds are compounds that are composed of discrete ions or charged species. There could be elemental ions, atoms that have lost or gain electrons. Or they could be polyatomic ions: a discrete collections of atoms that have a charge. One of the most important ideas regarding ionic compounds is that they are not themselves discrete units. They are collections of thousands, millions, septillions,....of ions. When chemists talk about a water molecule, they are referring to a discrete collection of three atoms, two hydrogen and one oxygen, that are stuck together. You can image a single molecule of water (just those three atoms) floating in space. In fact, this is not a bad picture for water vapor. Ionic compounds are very different. The ubiquitous example of an ionic compounds is sodium chloride, NaCl. It is this huge collection of sodium cations, Na⁺ and chloride anions, Cl^-. However it is not just a single pair of these ions. It is an enormous number of them. The key is that the ratio of the two ions is always one to one. Thus the "formula unit" (note this is not the "molecular formula") is NaCl. One Na⁺ for every Cl^-.

Ionic compounds form large repeating structure of ions. This structure is known as a crystal lattice. It is a specific pattern in which the position of each ion is known in relation to the other ions. Here are two pictures of sodium chloride, NaCl. Each diagram tries to illustrate the relative positioning of the sodium ions (the smaller ones) and the chloride ions (the larger ones).

Each cation (the blue or purple smaller spheres) in the lattice is surrounded by six anions (the green spheres). So the positive charge of the cation is found in an extremely stable location as it is interacting with six adjacent anions. Similarly each anion is surrounded by six cations. As a result the structure is a very low energy configuration for the ions. These pictures merely depict a small part of the overall structure as it repeats essentially forever.

Ionic compounds are usually combinations of metal and non-metal elements. The metallic elements generally form cations and the non-metal elements typically form anions. For example in NaCl, the cation, Na⁺, is formed by loss of an electron from the group 1 metal sodium. While the chlorine anion, Cl^-, is formed by the gain of an electron by the group 7 non-metal chlorine atom. The compound is composed of a one to one ratio of these two ions. Other compounds exhibit different ratios of cations and anions. For example in magnesium bromide, MgBr₂, the ratio of cation:anion is 1:2. Magnessium is a group 2 metal that forms cations with a stable noble gas electronic configuration when it loses its two valence electrons. Bromine forms a stable noble gas electronic configuration when it gains one electron. Thus we find magnesium as 2+ cation and bromine as a 1- anion in a 1:2 ratio in the compound. The resulting net charge for the compound should be neutral.

Ionic compounds are not all combinations of metals and non-metals. There are a large number of ionic compounds where one of the ions is a polyatomic ion. This is a collections of atoms that are "covalently bonded" together, but where this collection carries with a positive or negative charge. A list of common polyatomic ions can be found here . For all of the ions on this list you should know both their names and formula.

Ionic Bonding

Ionic bonds are chemical bonds in which we assume the electrons have fully "moved" from one element in the compound to another. This transfer of electrons from one species to another leads to ions. Elemental ions are elements with either less/more electrons that the neutral atom. Atoms that have "lost electrons" will have a positive charge and are called cations. Atoms that have gained electrons have a negative charge and are called anions. As positively and negatively charged particles are attracted to one another combinations of cations and anions form compounds that are held together by this electrostatic force. We refer to this as an ionic bond. The net effect for forming an ionic bond between two atoms is the sum of all of the "parts" of making the two ions from the elements and the energy of bringing them together. In general we can think about this as the sum of three processes.

The energy required to form the cation. This is the ionization energy for the element that is losing the electron(s).

The energy that is gained by forming the anion. This is electron affinity for the element that is gaining the electron(s).

Finally there is the energy that is gained by bringing the cation and anion together. This is called the lattice energy and is related to Coulumb's law.

Let's look at these three terms for an example compound of potassium chloride, KCl. Potassium chloride is a compound with a one to one ratio of K⁺ ions and Cl^- ions. The energy of the formation of this bond can be estimated by looking at the three terms above.

The ionization of all elements is positive (endothermic, \(+\Delta H\) ). This means we need to put this amount of energy in to form the ion. The first ionization energy of potassium is 419 kJ mol^-1. Note: this is the energy to form a K⁺ ion in the gas phase from a K atom in the gas phase. Here energy is absorbed.

The electron affinity of chlorine is 349 kJ mol^-1. This means that 349 kJ mol^-1 of energy are given off by the atom as a result of the ionization. Here energy is released (exothermic, \(-\Delta H\) ).

You'll notice that the energy required to form the cation is more than the energy released upon the formation of the anion. This means forming K⁺ and Cl^- from their gaseous atoms should be up-hill in energy. This process will require a net input of energy. However, we have left off a key piece of this process. The cation and the anion will be strongly attracted to one another. If we move them close to each other this will greatly lower their energy.

This is the third step in the process: the energy released as a result of stabilizing the ions by bringing them together. This is the energy of crystallization. Here energy is released (exothermic).

Here we are taking the gas phase ions and bringing them together to form a crystalline solid. Now the cations are sitting in postions surrounded by anions (and vice versa). This greatly lowers their potential energy. We typically quantify this energy by the reverse reaction. How much energy does it require to transform the crystalline solid into gas phase ions? This is the lattice energy

The lattice energy is positive as it is an absorption of energy. It is exactly equal to but opposite in sign of the energy of crystallization. For KCl the lattice energy is 715 kJ mol^-.

What happens if we put this all together? We can now judge which is lower in energy, the isolated atoms in the gas phase or the ionic compounds solid?

The net effect is the sum of these three terms. The energy in from forming the cation, +419 kJ mol^-. The energy out from forming the anion -349 kJ mol^-. And the energy out from forming the crystal lattice of -715 kJ mol^-. The total effect is now easily calculated: [+419 +(-349) + (-715)] = -645 kJ mol^-1. This means that the ionic solid (KCl) is 645 kJ/mol lower in energy than the same amount of the elements used to make it. You should conclude from all this that ionic compounds are generally very stable because they are at a much lower energy state than the elements that make them.

Ionic Radii

Ionic radii follow similar trends to atomic radii with one critical difference. Cations have very different radii than anions. Cations are all smaller than their neutral analogs while anions are all larger. This is easy to understand since cations have lost electrons. As a result they have both fewer electrons in the highest energy atomic orbitals farthest from the nuclei and the remaining electrons feel a stronger pull from the nucleus. Look at Na⁺ which is isoelectronic with Ne. It goes from being one of the "largest" atoms on the left-hand side of the periodic table to effectively one of the smallest with an electron configuration that is the same a neon (all the way on the right hand side). Moreover, Ne has a nuclear charge of Z=10 and Na⁺ has a Z=11. Thus the Na⁺ should be smaller than Ne. However as atomic radii and ionic radii are often defined differently then this comparison is difficult to make.

The general trends will continue to hold. From top to bottom of the periodic table ions will increase in radii. However, now left to right the radius is more of a function of the number of electrons. Mg²⁺ is smaller than Na⁺. Both have 10 electrons but Z=12 for Mg and Z=11 for Na. Similarly, O^2- will be larger than F^- as both have 10 electrons but Z=8 for oxygen and Z=9 for fluorine.

The following chart so both the atomic and ionic radii for some common ions. You can see the most dramatic differences are generally found in the trend top to bottom.

Coulomb's Law

The net effect for forming an ionic bond between two atoms is the sum of all of the "parts" of making the two ions from the elements and the energy of bringing them together. However, we can understand a lot about ion compounds simply by thinking about the interactions of the two ions (assuming they were already formed somewhere in the world).

The potential energy of two charges interacting is given by Coulomb's Law. This states that energy is related to the charges and the distance between them where

where \(q_1\) and \(q_2\) are the charges on the ions and \(r\) is the distance between them. \(\epsilon \) is the dielectric constant which for vacuum (gas phase) is simply equal to one. Thus if one charge is positive and the other is negative the energy of this interaction will be negative. That is to say, the two ions will have a lower energy (be more stable) when they are close together than when they are far apart. The magnitude of this energy depends on the size of the charges and the distances between them. Larger charges will have stronger interactions and lower energies. Likewise smaller ions will be able to get closer together and thus will have lower energies. Sometimes we take these two ideas and combine them into one we call charge density. How much charge is in a space. The larger the charge the larger the charge density. The smaller the ion the larger the charge density.

For example, the lattice energy of LiF will be higher than that of KF. Since Li⁺ is smaller (has a higher charge density) than K⁺, the ions in LiF are at a closer separation than the ions in KF. Similarly the lattice energy of NaF is higher than NaBr since, F^- is smaller than Br^-.

Coulomb's Law looks at the interaction of only two ions. In ionic compounds, we have a lattice that is composed of many ions all of which are interacting. The energy that is released upon forming the lattice from separate ions is the called the lattice energy. This essentially is the difference in energy for the separated ions compared to the ions in the crystal lattice. The lattice energy is complicated as it depends on the structure of the crystal. However, in general if we have similar crystal structures, then the differences between different ions will be given by the difference in the Coulomb energy. So we can approximate the magnitude of the lattice energy as simply being proportional to the Coulomb energy.

The lattice energy is defined as the energy required to separate the crystalline solid into gas phase ions as is shown in the example below for KCl.

For KCl the lattice energy is 715 kJ mol^-1. This is a lot of energy. As a result chemists will often say that ionic bonds are very strong. This is because they are referring to this particular situation of taking the solid and turning it into gas phase ions.

In contrast, you will often hear in biology that ionic bonds are the weakest bonds! This because they are generally talking about chemistry in a very specific context: aqueous solutions.

Chemistry is water is very different. Now if you are looking to break apart ions they are not ending up in the gas phase but instead they are "aqueous" or surround by water molecules denoted by the (aq) in the equation. This stabilizes their energy making it much less difficult to break apart the ionic solid. Additionally, the interactions between the ions is not in a vacuum but instead takes place in water. The dielectric constant, \(\epsilon\), for water is about 80. This means the attractive force and potential energy are effectively 80 times lower in water than in the gas phase.

Test Yourself

Which would you expect to have the lowest lattice energy (assuming they all form similar crystal structures)?

(hover/touch choice to get feedback on that choice)

KCl
NaCl
LiCl
RbCl

Covalent Bonding

In a covalent compound the electrons are shared between the atoms in the compounds. This "sharing" is not always equal, but it does not result in full excess electron charges residing on one atom compared to another. Instead the electrons are distributed about the entire molecule in such a way the minimizes their energy compared to their energies in the separate atoms. This is the key idea. The energy of the molecule is lower (more stable) than the energy of the separated atoms. We typically discuss this in terms of the potential energy. Often this is represented graphically where we look at the potential energy as a function of distance between the two atoms that are "bonding". If there is a distance at which the energy is lower than the two separated atoms we say these two atoms form a chemical bond. The bond length is the distance at which the potential energy is a minimum. The bond strength is the difference in the energy at the minimum compared to the separated atoms. This is shown on the diagram below.

This diagram show the energy for two hydrogen atoms as as function of the distance between them. There is a clear minimum at 74 pm (0.74 Å). We would say the bond length is 74 pm. The bond strength is the depth of this "well" which is 436 kJ mol^-1. That is the amount of energy the H₂ molecule would need to gain to break the bond and end up as two separate H atoms. Note the that while the two H atoms are attracted to each other at long distances (there energy is lower as the distance gets shorter), they are repulsive at very short distances (the energy is lower if the distance increases). This is due to the overlapping of the electrons in the two system (and repulsion of the two nuclei).

Bond Length and Bond Strength

There is a general trend between bond length and bond strength. Usually, the shorter the bond the stronger the bond. The longer the bond the weaker the bond. Is this always the case? No, it is usually the case. That is why we call it a trend. It is a particularly useful idea for similar bonds. For example a carbon oxygen single bond, C-O, is both longer and weaker than a carbon oxygen double bond, C=O.

Below is a widget in which you can look at the potential energy curves for dihalides (F₂, Cl₂, Br₂, I₂). Play with the widget to determine if this trend holds true for all the dihalides or only some of them.

Electronegativity

Electronegativity describes the relative pull of the a particular elements on the electrons in a covalent compound. There are several electronegativity scales that have been developed over the years to describe bonding. Some are based on elemental properties (ionization energy and electron affinity) other are based on bond strength measured in various compounds. However, all the scales share the same qualitative idea. The higher the electronegatively the greater the attraction the electrons have for that element. Since the scale is relative (a comparison between different atoms) F is typically chosen as the most electronegative atom and its electronegativity is set at 4.0. Electronegativity has a periodic trend that is nearly identical to that of ionization energy. It decreases top to bottom and it increases left to right. The reason behind this is nearly identical to that of ionization energy. The pull of the nucleus increases left to right and decreases top to bottom. Below is a scale of electronegativities. To calibrate the diagram F = 4.0 and Cs = 0.8

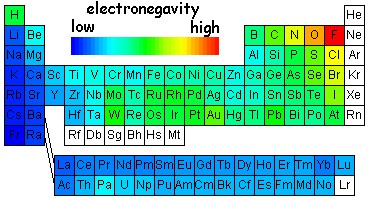
You can see a few exceptions to the strict increases left to right and decreases top to bottom (particularly in the transition elements). However in general, the upper right is the highest and the lower left is the lowest. Another notable outlier is hydrogen. Because hydrogen has only one electron, it is quite different from the other elements. Its electronegativity is nearly identical to that of carbon.

Polar Covalent Bonds

Electrons in covalent compounds are rarely exactly equally "shared" by all the atoms. Rather the electrons have a greater relative attraction for some of the atoms compared to others. As a result the electrons are not equally distributed throughout the molecule resulting in partial negative charges in some regions (those with a great pull of electrons) and corresponding partial positive charges in the regions that are deficient in electrons. We determine where these charges are by comparing electronegativities.

The Electronegativity of an element describes its relative "pull" of electrons in a covalent compound compared to other elements. High electronegativity elements will attract electrons more than low electronegativity elements.

The resulting covalent bonds then have a "polarity". That is to say one end is positive and one end is negative. This polarity is described quantitatively as a dipole moment. This is a measure of two charges separated by a particular distance.

Depending on the geometry of a molecule, the entire molecule may (or may not) have a dipole moment. This is a quantity that we can measure in the lab as an observable. Molecules with large dipole moments we call "polar". Those with very small or no dipole we call "non-polar". This topic is explored in greater detail later when examining molecular shapes.

Polar vs Ionic Bonds

We often lump bonds into being either ionic or covalent. But this greatly simplifies what is again a complex quantum mechanical problem. Luckily our over simplification gives us the correct perspective much of the time. None the less, it is important to realize that this actually is a spectrum of different types of bonds ranging from what we would call purely covalent to ionic. In between, bonds might be best described as partly ionic and partly covalent. For such compounds we talk about their "covalent character" or "ionic character". Thus NaCl is something in which we would say the bonding is dominate by the ionic character. We can qualitatively lump bonds into these different categories by differences in electronegativities. Large differences lead to ionic bonds (bonds with mostly ionic character) while small differences lead to covalent bonds (bonds with mostly covalent character). Before we simply said ionic bonds form between a metal and a non-metal, and covalent between a non-metal and a non-metal. However, looking at electronegativity differences, you see that this is the same idea as non-metals have larger electronegativities than metals.

We then further divide up the covalent bonds into two categories. Pure covalent and polar covalent. Pure covalent are bonds between two elements with identical electronegativities. For these bonds the electrons are perfectly equally shared between the two atoms. Polar covalent bonds form between elements with different electronegativities but those that aren't large enough that we could call the bonds ionic. For example the bond between hydrogen and chlorine. Chlorine has a larger electronegativity so we would expect this bond to be polar with more of the electrons residing on the chlorine. To denote this in a structure we would draw a small partial charge on the atoms using a lower case delta, δ, with a plus or a minus sign. The element with the higher electronegativity will have a greater share of the electrons and thus it will be the δ-. Note, the charges are partial. This implies that the electron spends more time "on that atom" but is not completely transferred (that would be the ionic picture).