The layout of the periodic table is organized such that various physical and chemical properties of the elements show distinct trends or patterns. Knowing these trends helps one to make informed decisions about the anticipated properties of a given family in the periodic table.
The trends can be understood in terms of two key concepts.
First, is the electronic configurations of the elements. The valence electrons for elements in each group as essentially the same. This means that we can expect them to have similar chemistry since they have similar electron configurations.
The second idea is relating the properties of the valence electrons to the strength of their interaction with the nucleus. The nuclear charge is of course the same for all of the electrons in an atom. However, we can understand some complex interactions in atoms based on some simple ideas that assumes that the valence electrons experience a different nuclear charge than the core electrons. We refer to this reduced nuclear charge as "the effective nulcear charge". Effectively nuclear charges varies fairly systematically across a period and down a group, thus the idea of periodic trends. There are always excepts to these trends. These exceptions are related to the actual details of the quantum mechanics in these system that are glossed over in such a simplistic approach.
When we look at trends in the periodic table, we see a clear pattern in which there is a huge change in properties between the noble gases and the alkali metals. This is despite the fact that they are different by only one electron and one proton. From this we arrive at the idea that we can think of the electrons in an atom as being "layered" into shells as we fill up different n levels. The noble gas configurations are the filled shells and represent the lowest energy most stable configurations. After this, the next electron is forced into a higher energy orbital. This alone would not account for the dramatic difference we see because the energy difference between say a 2p electron in Neon and a 3s electron in Sodium shouldn't be that large unless there was another effect. This other effect is the idea of electronic shielding. The idea of shielding is simply that this outer most electron is shielded from the full nuclear charge because of the negative charges of the other electrons "between" it and the nucleus. In this way, we divide up the electrons between those in the stable nobel gas "core" and the new "valence" electrons outside this core. The valence electrons now experience a reduced or effective nuclear charge, Zeff < Z. One way to crudely estimate Zeff is to simply imagine that the core electrons are canceling out the charge of the nucleus so Zeff= Z - (# or core electrons). This over estimates the shielding (as this is the maximum one would every expect) and results in a Zeff that is too small. Never the less, it is good enough to predict the trends.
Here is an illustration showing how to "calculate" +5 as the effective nuclear charge (Zeff) for phosphorus.
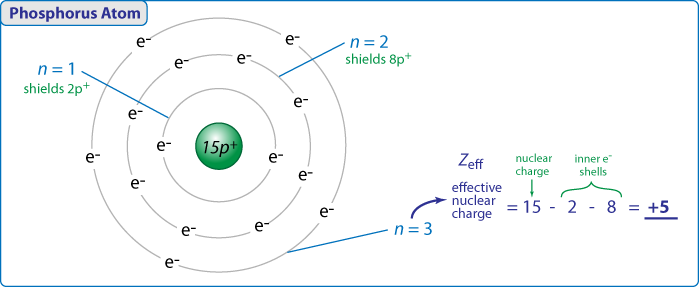
We are not implying that the electrons are in orbits here, this is simply showing inner shell electrons that shield the outer valence electrons from the full nuclear charge. This is a simple picture for us to try to visualize what are actually complex quantum mechanical behaviors. None the less, this simple idea offers good physical insight into the trends we observed in the periodic table. Moreover, this is a simplification of the idea of "shielding". More accurate attempts to quantify shielding would put the Zeff at 5.64 for the 3s orbitals and 4.89 for the 3p orbitals. You can see our hand wavvy guess is not too bad in this situation.
Shielding and Effective Nuclear ChargeIonization energy (I.E.) is the energy required to remove an electron from an atom in the gas phase. For example the ionization energy for a sodium atoms is defined as the energy for the following reaction
\[{\rm Na(g) \rightarrow Na^+(g)+e^-}\]
This is actually the first ionization energy as it is the energy required to remove the first electron. The second ionization energy is the energy required to remove an electron from the 1+ ion. For sodium the 2nd I.E. would be
\[{\rm Na^+(g) \rightarrow Na^{2+}(g)+e^-}\]
It is important to note that the each subsequent ionization energy is always higher than the previous one as we are reducing the number of electrons but the number of protons is fixed. Thus, as we remove electrons and decrease the shielding and repulsion, the effective nuclear charge is increasing.
Finally, we can use the Rydberg formula to calculate the I.E. for hydrogen-like atoms since this is the energy need to go from the n=1 state to the n=infinity state.
One trend that is studied for atomic systems in the "atomic size". The size of an atom is difficult to define. This is because the wavefunction of an electron in an atom extends to infinity. However at some distance away from the nucleus the probability of finding the electron while finite is essentially zero. However, this "size" is chosen rather than being something that can be directly measured. Alternatively, atomic size can be determined based on experimental data. For example, the size of a chlorine atom might be deduced from the distance between two chlorine atoms in molecular chlorine, Cl2. The size of ions (atoms with a charge from either excess or missing electrons) could be deduced from the distances between the nuclei in a crystalline solid.
Since all atoms and ions are spherical, there size is typically given as a radius. The size of an atom (ion) is referred to as its atomic (ionic) radius. As noted above this radius could be determined in a number of ways. Therefore the absolute numbers you might find in a table can vary from source to source. However, the trends in atomic radii should hold regardless of how the radius is defined.
Atomic radii are related to the "radial distribution function" we saw for the wavefunctions (atomic orbitals). Those told us the probability of finding an electron at a particular radius. The trend for atomic radii will hold for the most probable distance from the radial distribution function with the caveat that atomic radii are typically derived from the highest energy valence electrons.
Finally, despite the trends atomic radii are all quite surprisingly similar. The balance of adding both protons and electrons to different elements helps to generally balance the interactions in the atoms. Thus even the largest of atoms like cesium at 2.98 x 10-10 m while the smallest helium is 3.1 x 10-11 m. This is a difference of only a factor of ten. The vast majority of the atoms have a size that is about 10-10 m. This unit of length has its own name, an Ångstrom, which is defined as 1 Å is equal to 1 x 10-10 m (0.1 nm). This is the "size of a typical" atom.
Electron affinity (EA) is the energy released from an atom upon the addition of an electron to form the anion. This is defined for atomic species in the gas phase. For example the electron affinity for fluorine is the energy released in the following reaction.
\[{\rm F(g) + e^- \rightarrow F^-(g)} \]
Often electron affinity is treated in a similar way as ionization energy. As such, it is often taught as if it has a similar predictable periodic trend across and down the periodic table. However, electron affinity has essentially no periodic trend. There are particular places on the periodic table where atoms have a finite electron affinty, and others where the EA is zero. These places are where adding another electron will give an atom an electron configuration that is either a filled a shell (or subshell) or half fill a subshell. The largest EA are occur when fillng a shell. Thus the halogen atoms (group 7) have large EA. Fluorine has a large EA (it does go down slightly as you move down the periodic table but Cl is actually bigger than F). Carbon has a reasonalbe EA as adding an elecron would give it a half-filled p subshell. Nitrogen in constrast has no EA since it already has a half filled p-subshell. Likewise the EA of Zn, Cd, Hg are all zero as they have a filled d-subshell. Cu, Ag, and Au are all fairly large as adding one electron will fill the d-subshell. This makes the trend left to right on the periodic table spotty at best. However, elements in the same group (with similar valence configurations) are similar to each other.
There are two trends that we are focussing on for periodic trends moving from the top to the bottom on the periodic table in the same group. They are both related to the fact that as you move from top to bottom, the effective nuclear charge, Zeff, is essentially constant, but the valence electrons are in higher and higher n shells. This means the valence electrons are farther from the nucleus as you go down the periodic table. This leads to a larger radius and a lower ionization energy. Note: this is a general trend that tends to hold better than the trends left to right. Also, it is difficult to compare the magnitude of the trends left to right and those top to bottom so it is best to keep comparison in the same period or the same group.
Periodic Table Trends from Top to BottomThere are two trends that we are focussing on for periodic trends moving left to right on the periodic table in the same period. They are both related to the fact that as you move from left to right the effective nuclear charge, Zeff, is increasing. This means the valence electrons feel a stronger attraction to the nucleus. This leads to a smaller radius and a higher ionization energy. Note: this is a general trend and there are some small exceptions. These typically arise for elements with either full sub-shells or half-filled sub-shells.
Periodic Table Trends from Left to Right