Pressure is an important property (state function) of a gas (or any substance for that matter). Pressure is a measure of the force per area that substance exerts on its surroundings. Technically it is the force per area applied in the direction perpendicular to the surface of the object.
There are a number of ways to measure pressure. These include instruments that directly measure the force of the gas, to those that detect the number of gas particles and convert this to a pressure. Knowing about how pressure is measured can help with some of the unusual units that are used for pressure. The "best" unit for pressure is a Pascal (Pa). This is a force of 1 Newton (N) per square meter (m2). However, it turns out that this is a small pressure compared to the typical values we encounter in chemistry. The most typical pressure is the prevailing pressure of the atmosphere. This pressure varies day to day, but at some point an standard unit of 1 atmosphere (atm) selected. 1 atm = 101,325 Pa. As such, atm is a historic unit that still gets a lot of use, however it is not easily converted to kg, m, and seconds. A "better" unit is the bar. 1 bar is chosen to be close to 1 atm and is defined as be equal to 100,000 Pa or 100kPa. 1 atm = 1.01325 bar.
Historically pressure was measured in a barometer (or manometer). This instrument could measure the pressure by measuring a differential in a force applied to a liquid. For a barometer, the liquid is exposed to the atmosphere and is forced up into a long sealed tube. The height that the liquid rises in the tube is then a measure of the force applied from the atmosphere. The height depends on the pressure applied and the density of the liquid such that:
\[P = {\rho gh}\]
Where g is the gravitational acceleration constant, P is the pressure, and \(\rho\) is the density of the liquid. If the gravitational acceleration constant has units of m s-2 (9.8 m s-2) and the density is in kg m-3 the pressure will be in Pascal. Because most barometers employ mercury as the liquid (since it is dense and has a low vapor pressure) the height of the liquid is often used as a measure of pressure. Thus millimeters of mercury (mmHg) or centimeters of mercury (cmHg) are sometimes used as units for pressure. Torr is another historical name for mmHg. 1 mmHg is approximately 1 Torr. Torr are strictly defined such that 760 Torr = 1 atm.
Boyle's Law states that the pressure (P) of a gas is inversely proportional to the volume (V). This law is valid as long as the temperature and the amount of gas are constant. Any units will work here:
\[P\,V = k \hskip12pt{\rm (constant)}\]
The constant, \(k\), will depend on the number of moles and the temperature. As long as those two state functions are constant, \(k\) will be a constant and Boyle's Law will hold. Below is a plot of pressure vs volume (aka: a PV plot). Note the shape of the plot, this is a classic inverse relationship.
Most Boyle's Law problems have an initial set of conditions (P1 and V1) and then a final set of conditions (P2 and V2). BOTH conditions must satisfy Boyle's Law and therefore:
\[P_1V_1 = P_2V_2\]
Any units will work here for pressure and volume - just make sure the units are the same on each side of the equation.
Below is a Boyle's Law applet like the syringe we played with in class that allows you to explore the relationship between pressure and volume along with a graph of the data.
Charles's Law states that the Volume (V) of a gas is directly proportional to the temperature (T). This law is valid as long as the pressure and the amount of gas are constant. The temperature must be an absolute temperature:
\[{V \over T} = k \hskip12pt{\rm (constant)}\]
The constant, \(k\), will depend on the number of moles and the pressure. As long as those two state functions are constant, \(k\) will be a constant and Charles's Law will hold. Below is a plot of temperature vs volume for an ideal gas. Note that the line is linear which is consistent with a direct proportionality.
Most Charles's Law problems have an initial set of conditions (V1 and T1) and then a final set of conditions (V2 and T2). BOTH conditions must satisfy Charles's Law and therefore:
\[{V_1 \over T_1} = {V_2 \over T_2}\]
Any units will work here for volume but the temperature must be absolute (Kelvin) .
Avogadro's Law: The volume of a gas is directly proportional to the amount of gas. The typical amount of gas is in moles. Avogadro's Law assumes that temperature and pressure are constant.
\[{V\over n} = k \hskip12pt{\rm (constant)}\]
Where \(n\) is in moles of gas.
As with the other gas laws (Boyle's and Charles'), Avogadro's Law is typically depicted when considering an initial set of conditions (condition 1) and a final set of conditions (condition 2).
\[{V_1\over n_1} = {V_2\over n_2}\]
This is exactly like Charles' Law except the temperature (T) has been replaced with number of moles (n).
Also keep in mind that mass is proportional to moles which means the mass of the gas can also be used here:
\[{V_1\over m_1} = {V_2\over m_2}\]
Where m is the mass of the gas. However, keep in mind that unlike for n, the two conditions compared with the mass must compare the same gas (as different gases have different molar masses).
The classic combined gas law is a combination of Boyle's Law and Charles' Law. The relationship between pressure, volume, and absolute temperature are all present in the combined gas law. It is written mathematically as:
\[{P V \over T} = k \hskip12pt{\rm (constant)}\]
The constant, \(k\), will also depend on the number of moles and could therefore vary. As long as the number of moles is constant, \(k\) will be a true constant value.
Most combined gas law are worked with a before condition and an after condition. We typically number these conditions of state as 1 and 2 (sometimes initial and final also). So the working form of the combined gas law is:
\[{P_1 V_1 \over T_1} = {P_2 V_2 \over T_2}\]
Any units will work here for pressure and volume but the temperature must be absolute (Kelvin).
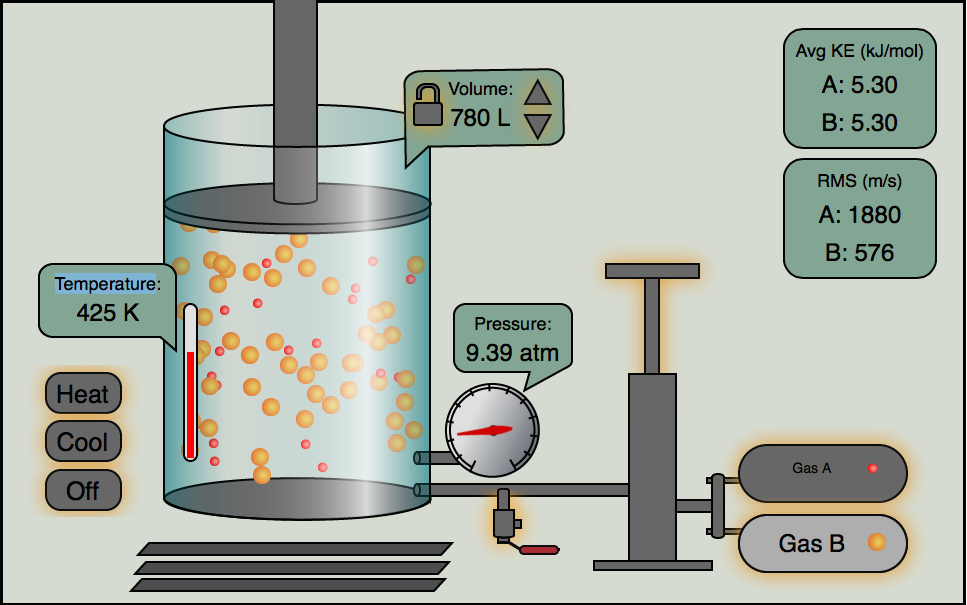
Click the image below and you can play with our gas simulator. You can control the relative amounts of two gases, A and B with the pump handle. You can release gas with the release valve. The temperature can be raised and lowered, plus you can have volume locked or change. Play around with it and notice the relationships of \(P, V, n, and\;T\).
This only works with Flash enabled devices (no iPhones or iPads)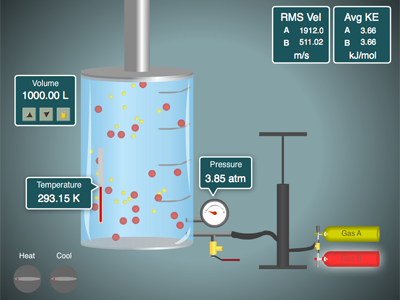
If you have a device without a Flash plug-in (iPhones and iPads, etc...) you can still run the simulator on this Javascript Gas Law Simulator