The kinetic theory of gases is a general idea that we use to describe two key concepts.
\[ PV = nRT \]
We find that if we examine the velocities of particles in a gaseous sample experimentally, that not all of them are moving at the same velocity.
There is a distribution of velocities. We refer to this distribution as the Boltzmann distribution (or more correctly the Maxwell-Botlzmann distribution).
There are three key ideas that you should take away regarding these distributions.
1. The distribution of velocities is assymmetric. There is a peak and long tail to higher velocities.
2. Both the average velocity and the width of this distribution are temperature dependent. The higher the temperature the faster the average velocity and the broader the distribution.
3. The distribution also depends on the mass of the particles. The lighter the particle (less massive) the faster the velocities and the broader the distribution.
Below is a graph of the different distribution for several nobel gases. Notice the heavier gases are slower than the lighter ones.
The key to the kinetic theory of gases is the notion that the average kinetic energy (\(E_{\rm k}\)) for the particles in a gas sample is proportional to the temperature. There are two key ideas here. First, the average \(E_{\rm k}\) is the "average" since not all the particles will have identical energies. Some will be lower than average. Some will be higher than average. etc...The second important idea is that \(E_{\rm k}\) is proportional to the absolute temperature. Double the temperature and you'll double \(E_{\rm k}\). Go to a temperature of zero Kelvin and you'll be in a situation with zero \(E_{\rm k}\)!
Better we know the absolute relationship.
\[E_{\rm k} = {3\over 2}R\,T\]
Where \(R\) is our friend the Universal Gas Constant. It turns out the \(R\) is much more important than for simply looking at ideal gas behavior. It is actually related to the proportionality between \(E_{\rm k}\) and temperature. You may have seen a similar relation in the past
\[E_{\rm k} = {3\over 2}k\,T\]
This is an identical relation with different units. The constant \(k\) is Boltzmann's constant and is used if one is looking at the energy of a single molecule. If you are looking a the energy of 1 mole of a substance we use \(R\). The two are identical except for units. To get from molecules to moles we simply multiply by Avogadro's number
\[R = k\,N_A\]
So when looking at the Kinetic energy formula with \(R\) you want to get units of molar energy. While L-atm (or L-bar) are energy units, they are a bit strange. So for any \(E_{\rm k}\) relation involving \(R\) stick with the gas constant in the units of Joules.
\[R = 8.314\;{\rm J\;K^{-1}\;mol^{-1}}\]
Since we now know how to relate temperature and kinetic energy, we can relate temperature to the velocity of gas molecules. Note since these are distributions the values (\(E_{\rm k}\) or velocity) that we are talking about are always averages.
\[E_{\rm k}={3\over 2}\,R\,T\]
\[E_{\rm k}={1\over 2}\,m\,v^2\]
setting these two equal and solving for the average square velocity we get
\[v^2 = {3\,R\,T \over m}\]
The root mean square velocity or \(v_{\rm rms}\) is the square root of the average square velocity and is
\[v_{\rm rms} = \sqrt{3\,R\,T\over M}\]
Where \(M\) is equal to the molar mass of the molecule in kg/mol. The root mean square velocity is the square root of the average of the square of the velocity. As such, it has units of velocity. The reason we use the rms velocity instead of the average is that for a typical gas sample the net velocity is zero since the particles are moving in all directions. This is a key formula as the velocity of the particles is what determines both the diffusion and effusion rates.
Below is a problem examining the ratio of the velocities for two different molecules at the same temperature.
The rates of diffusion and effusion both depend on the velocities of the gas molecules. As such their mass and temperature dependence are identical to that of the rms velocity. Diffusion and effusion are two distinct but similar gas behaviors. Diffusion is the spreading out of molecules away from a concentrated region due to the random motions of the gas particles. Think of an "odor" wandering across a room. The rate of diffusion of a gas depends on how fast the gas molecules are moving. Faster rms velocities leads to faster diffusion.
Effusion is a very specific sort of gas behavior that is the rate of a gas escaping a container through a small pore. The rate that this happens depends on how many gas molecules "collide" with the pore. This depends directly on the rms velocity of the gas. This seems like a random behavior to ever think about, but it is a phenomenon that most everyone has experience in the "deflation" of a He balloon. Most balloons are actually porous (with the holes being very very small). However, over the time the He atoms find the holes and escape. Thus the entire industry of mylar balloons which are significantly less porous.
For diffusion and effusion one can try to derive "new formulas" that relate relative rates to molecular mass, but they are all just a recasting of the rms velocity since
\[{\rm Rate \; of \; Diffusion} \propto v_{\rm rms}\]
\[{\rm Rate \; of \; Effusion} \propto v_{\rm rms}\]
Now that we can relate temperature to kinetic energy and gas velocity, we can use these idea to derive a relationship between all the other gas properties (specifically volume, pressure, and the number of particles).
To this end we start out with a few assumptions.
Now we simply have to do a fairly difficult physics problems to solve for the pressure felt by the walls of the container that results from the collision of the molecules. This can be found in detail here . However, without going through all the math we can arrive at a few conclusions ourselves. First, the pressure results from the number of collisions that occurs per unit time as the "impact" of those collisions. The number of collisions will be proportional to the velocity of the particles and the impact depends on their momentum (the product of mass and velocity).
Let's use this idea to examine the relationship between \(P\) and \(n\). The impact of the collision will be unchanged as we change the number of molecules. However, the number of collisions will scale directly with \(n\). Therefore we find
\[P \propto n\]
Similarly the volume,\(V\), will have no effect on impact, but as the volume increases the number of collisions will decrease proportionally. So we find that
\[P \propto {1 \over V}\]
Finally, we can look at \(P\) and \(T\). Changing the temperature changes velocity that affects both the number of collisions as well as the "impact". However since velocity is proportional to \(\sqrt {T}\) we find that
\[P \propto T\]
When we put this all together (and we actually do the math/physics part) we get a quantitative result that yields
\[PV=nRT\]
This is the ideal gas law now derived as a physical model rather than simply arrived at from empirical data at low pressures. Most interesting is now it provides us some "physical insight" into gas behavior. When gases are behaving ideal, our assumptions that lead us to our derivation must be quite accurate. Thus at low pressures where the ideal gas law holds the best, the molecules must be far apart and essentially occupying a negligible volume (assumption 1). In addition, they must not be interacting at all (assumption 3). What happens at high pressure when the ideal gas law begins to fail? The molecules get closer and closer together. Now their volume cannot be ignored (assumption 1 fails) and they begin to interact (assumption 3 fails). Thus even in the failures of the ideal gas law, we can learn something about the behavior of gases.
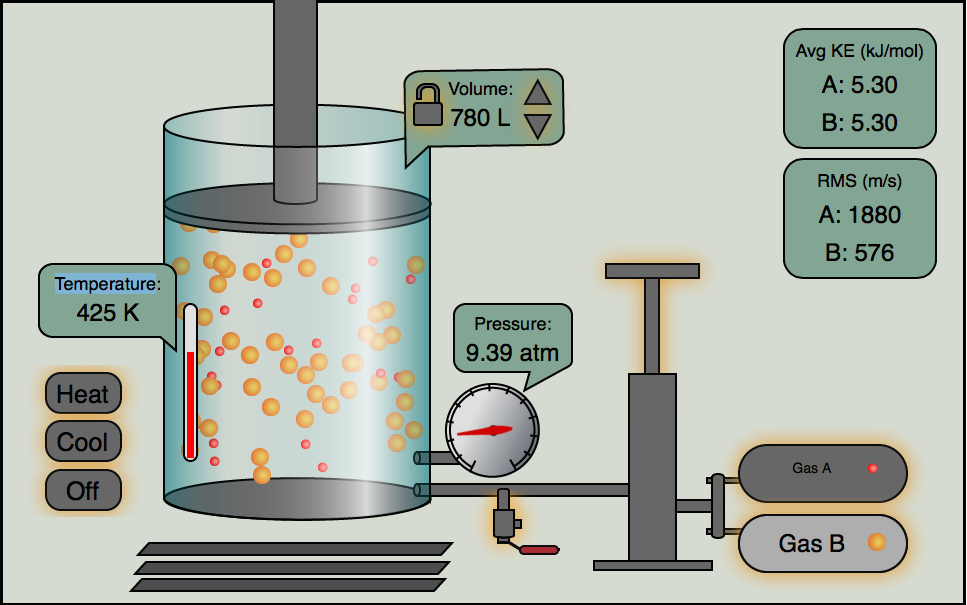
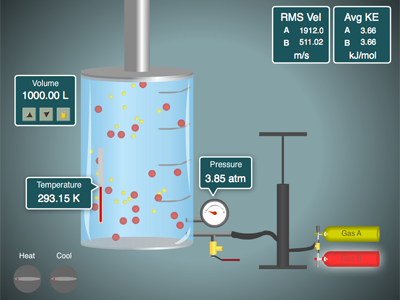
Click the image below and you can play with our gas simulator. You can control the relative amounts of two gases, A and B with the pump handle. You can release gas with the release valve. The temperature can be raised and lowered, plus you can have volume locked or change. Play around with it and notice the relationships of \(P, V, n, and\;T\).
This only works with Flash enabled devices (no iPhones or iPads)
If you have a device without a Flash plug-in (iPhones and iPads, etc...) you can still run the simulator on this Javascript Gas Law Simulator