
The valence bond model is a quantum mechanical model for understanding bonding in molecules. However, now it is mostly used by chemists as a means to describe the bonding with organic systems qualitatively. The idea is that bonds form between atoms as a result of the overlap of atomic orbitals. This leads to what we would call a localized bonding picture. You can point to a bond in a molecule and say what types of atomic orbitals lead to that particular bond. The only complication is that the atomic orbitals we know and love cannot lead to the geometries that we know molecules have. Thus, we have to invent new "hybrid" orbitals by making combinations of the atomic orbitals we started with (s,p,d,f orbitals).
When drawing large organic molecules with lots of carbon and hydrogen atoms it becomes tedious to draw all the atoms and bonds. So chemists have developed a shorthand notation. In this scheme, carbon atoms are assumed to exist between bonds, and hydrogen atoms are not drawn in at all. The number of hydrogen atoms for any carbon is "implicit" since carbon is assumed to always make four bonds (formal charge = zero).
Note also that in many line drawings, the lone pairs on atoms are also not shown but are "implicit." Only carbons can be at the end of lines intended as bonds - all other atoms except hydrogen must be shown.
See this animated example below that has the line drawing, then puts in the carbons, then adds the hydrogens and the lone pairs.

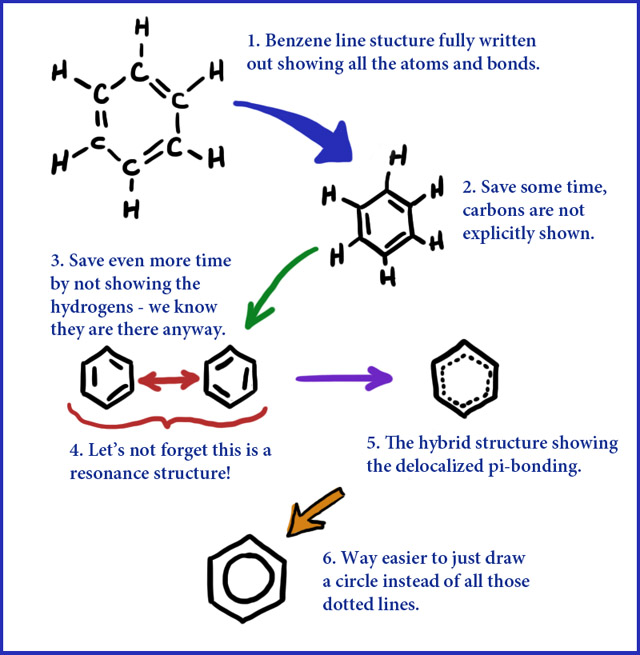
This shorthand for structures is maybe at its best for benzene (C6H6). All the carbons in benzene are sp2-hybridized and a delocalized π-system is formed. The following picture/diagram shows the step-by-step "evolution" of taking the full structure all the way down to the simple ring-in-a-hexagon structure. One big advantage of this structure is that not only is it much faster to draw but it avoids the huge misconception that there are single and double bonds flipping back and forth. The bonding is delocalized around the ring with all the carbon/carbon bonds being equal.
Valence Bond theory is a localized theory of chemical bonding. Again VB theory is a quantum mechanical theory that is now mostly used as a qualitative description of chemical bonding (in particular in organic molecules). It describes the bonds in molecules as arising from the overlap of atomic orbital centered on the atoms in the molecule. However, to achieve the correct geometries it must often use new "hybrid" orbitals that result from the mixing of some number of pure atomic orbitals. These new "hyrbridized" orbitals are degenerate (have the same energy) that is intermediate to the pure atomic orbitals. These new hybridized atomic orbitals occupy the correct regions in space that allow for the given electronic geometry around the atom such that head-on overlap can occur between individual atoms to give sigma bonds.
We use VB theory to describe the orbitals that give rise to the sigma and pi bonds in a molecule. Even though we often use VB merely as a qualitative theory it provides new insights into chemical bonding beyond what can be achieved from simple picture such as Lewis dot structures or VSEPR. For example, the VB model gives a better picture in particular of how to understand double bonds in a molecule as well as how to describe molecules that exhibit resonance.
The first hybrid orbitals we are going to look at are the sp3 hybrids. They get their name from the fact that they are a combination of one s atomic orbital and three p shaped atomic orbitals. As the original orbitals are simply mathematical functions (that describe the wave that is the electron), these new hybrids are simply new mathematical functions that are combinations of the old ones (the old ones added together in various ratios). When making hybrid orbitals, you make as many hybrid orbitals as the number of atomic orbitals you start with. Thus one s and three p's is four total atomic orbitals (AO). This makes four sp3 orbitals. These orbitals are arranged in space such that they point at the corners of a tetrahedron. That is they have a tetrahedral geometry. Thus, we would say that any atomic center that has an electronic geometry that is tetrahedral is sp3 hybridized.
The four sp3 orbitals all have the same energy and they all lie somewhere between the energy of the s and p orbitals that were used in the hybridization.
Like sp3, sp2 hybrids are a combination of s and p atomic orbitals. In this case, you take one s and two p orbitals to make three sp2 orbitals. These three orbitals are arranged pointing out from the atomic center in a trigonal planar arrangement.
Thus, any atom with an atomic center that has a trigonal planar electronic geometry is sp2 hybridized.
Because only three of the four atomic orbitals are used to make the sp2 hybrid orbitals, there is one "extra" p orbital remaining on the atomic center. This p orbital can overlap with neighboring p orbitals to form a π bond. Thus, we have direct overlap of orbitals that leads to sigma bonding and "side-on" overlap that leads to pi bonding. Any double bond is described as one sigma bond plus one pi bond. This pi bond can only form if the p orbitals "line up" with each other. This means that double bonds cannot rotate, as rotation of the molecule around this axis effectively breaks this overlap and destroys the pi bond. It is not that it can't ever happen. It just requires a lot of energy (it is like breaking a bond).
sp hybrid orbitals are a combination of one s and one p atomic orbital. This leads to two sp hybrid orbitals that are arranged in a linear geometry.
Thus, any center with a linear electronic geometry is sp hybridized.
As only one p orbital is "used," there are two "left-over" p orbitals on the atomic center. Each of these could overlap with an appropriately oriented p orbital on a neighboring molecule and form a pi bond. As there are two p orbitals, these could be double bonds or there could be a triple bond.
bipyramidal
octahedral
To achieve geometries with more than four electronic regions we need more than four orbitals. This requires using d orbitals. This is only possible for elements in row 3 and below.
The hybrids we make are sp3d, which is a trigonal bipyramidal structure, and sp3d2, which is octahedral in structure.