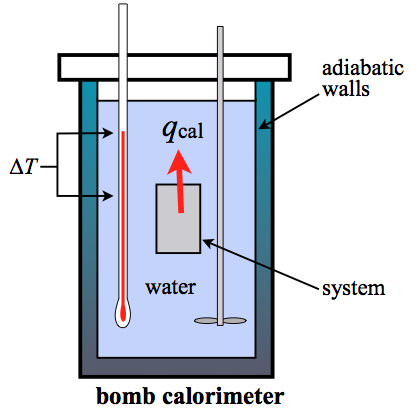
A bomb calorimeter is a constant volume calorimeter (constant volume is isochoric). So the heat measured by such an instrument is equivalent to the change in internal energy or \(\Delta U\). The heat can be determined from the temperature change, \(\Delta T\), and the heat capacity of the calorimeter, \(C_{\rm cal}\). For a bomb calorimeter, the heat capacity is usually quite large due to all the water and the hardware (stirring paddles, blades, the stainless steel "bomb" holding the reactants, the wiring, the walls of the calorimeter, etc...). This value is \(C_{\rm cal}\). It is used to find \(q_{\rm v}\) of the system:
\[q_{\rm cal} = C_{\rm cal} \Delta T = -q_{\rm v,system} \]
Sometimes, it is more convenient to split the overall heat capacity of the calorimeter into its component parts: (1) the water, and (2) the hardware.
\[C_{\rm cal} = C_{\rm hardware} + m_{\rm water} C_{\rm s,water} \]
The hardware heat capacity will be in units of J/K or kJ/K while the water heat capacity has to be calculated from the mass of the water and the specific heat of water (4.184 J g-1 K-1). So the water part is slightly variable due to the fact that you can fill the calorimeter up with slightly different masses of water each time you use it. If you put all that into one formula for a bomb calorimeter, you get:
\[q_{\rm cal} = C_{\rm hardware}\Delta T + m_{\rm water} C_{\rm s,water}\Delta T \]
One last thing to note. Many tables will list heat capacities using °C instead of K. Realize that these two units are equivalent in this context because we are using \(\Delta T\) and not plain \(T\). A change in Kelvin of 10 is exactly a change of 10 in °C as well. So don't try to change Celsius to Kelvin and vice versa here. This will be true throughout all your science courses.
Chemists are almost always interested in the enthalpy change to know what would have happened at constant pressure. It is possible to get \(\Delta H\) from a bomb calorimeter experiment. It just takes an additional step to do a conversion from \(\Delta U\) to \(\Delta H\).
To convert from \(\Delta U\) to \(\Delta H\) requires knowing the amount of work done (\(w\)) during the reaction. In the case of a chemical reaction, work can be easily calculated by simply counting the number of moles of gas products and gas reactants.
\[\Delta n_{\rm gases} = \Sigma n_{\rm gas\;products} - \Sigma n_{\rm gas\;reactants} \]
Now the work can be calculated with the formula:
\[{\rm work:} \hskip10pt w = -\Delta n_{\rm gases} R T \]
So this leads to the final formula for the conversion:
\[\Delta U = \Delta H - \Delta n_{\rm gases}RT \]
or with a little algebraic rearranging...
\[\Delta H = \Delta U + \Delta n_{\rm gases}RT \]