Calorimetry is simply the measurement of heat. This is typically done under two distinct conditions.
Either at constant pressure in which case
\[q=q_p=\Delta H\]
Or at constant volume in which case
\[q=q_v=\Delta U\]
The two instruments we typically discuss for these situations are: a coffee cup calorimeter (constant pressure calorimeter), and a bomb calorimeter (constant volume calorimeter).
In a calorimeter we take advantage of the fact that we can use the temperature change of water to quantify an amount of heat. A typical calorimeter works by simply capturing all the energy released (or absorbed) by a reaction in a water bath. The energy that enters (leaves) the water must be exactly equal to the energy released (absorbed) by the chemical reaction. Thus by measuring the change in the temperature of the water we can quantify the heat (enthalpy) of the chemical reaction.
Attached below is a helpful sheet on calorimetry from Dr. Paul McCord. When working calorimetry problems it is important to read the problem to see how the calorimeter is calibrated. Sometimes there is just the heat capacity of the calorimeter, other times you have to take into account the specific heat and mass of the water or solution in the calorimeter and the heat capacity of the hardware of the calorimeter (together they make the heat capacity of the calorimeter) and yet other times you can assume the heat capacity of the hardware to be zero (as is often the case with coffee-cup calorimetry BUT NOT ALWAYS!) and you just have to consider the specific heat and mass of the water in the calorimeter.
Here is Dr. McCord's Calorimetry Help Sheet
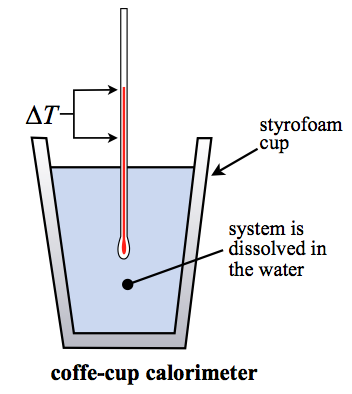
A coffee cup calorimeter is a constant pressure calorimeter. As such, the heat that is measured in such a device is equivalent to the change in enthalpy. A coffee cup calorimeter is typically used for solution based chemistry and as such generally involves a reaction with little or no volume change. Therefore, while the heat is exactly equal to the enthalpy change (\(\Delta H\)) in this case, it will also be approximately equal to the change in the internal energy (\(\Delta U\)) since the work will be very small (assuming there are no gas reactants or products).
The more technical name for this type of calorimetry is isobaric calorimetry. The "coffee-cup" name comes from the fact that most of the time this experiment is done inside of a simple styrofoam cup. A styrofoam cup makes for a good adiabatic wall and helps keep all the heat released or absorbed by the reaction inside the cup so we can measure it.
The heat capacity of a coffee cup calorimeter is typically taken to be that of the water in the calorimeter. However, it could be that the "hardware" and the water heat capacities have both been measured and you treat it much like in bomb calorimetry. None-the-less, most coffee-cup calorimeters have virtually no hardware (it's a styrofoam cup!) and you can ignore that component. So the equation of interest is:
\[q_{\rm cal} = m_{\rm water} C_{\rm s,water}\Delta T = -q_{\rm p,system} \]
Note that for such a measurement, the heat of the reaction is assumed to all go into the temperature change of the water. This is why the heat can be easily quantified using the mass of the water, the specific heat capacity of the water, and the temperature change. Since this measurement is at constant pressure (isobaric), the heat is equal to the change in enthalpy or \(\Delta H\). Note: be careful with the sign on \(\Delta H\). Heat out of the reaction is heat in to the calorimeter and vice versa. So an increase in temperature means the reaction was "exothermic" and \(\Delta H\) is negative. Conversely, if the temperature drops during the reaction, then the reaction must be endothermic and \(\Delta H\) is positive.
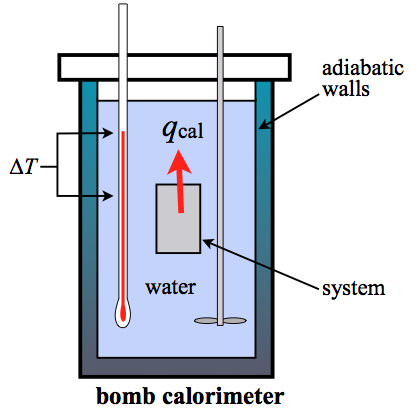
A bomb calorimeter is a constant volume calorimeter (constant volume is isochoric). So the heat measured by such an instrument is equivalent to the change in internal energy or \(\Delta U\). The heat can be determined from the temperature change, \(\Delta T\), and the heat capacity of the calorimeter, \(C_{\rm cal}\). For a bomb calorimeter, the heat capacity is usually quite large due to all the water and the hardware (stirring paddles, blades, the stainless steel "bomb" holding the reactants, the wiring, the walls of the calorimeter, etc...). This value is \(C_{\rm cal}\). It is used to find \(q_{\rm v}\) of the system:
\[q_{\rm cal} = C_{\rm cal} \Delta T = -q_{\rm v,system} \]
Sometimes, it is more convenient to split the overall heat capacity of the calorimeter into its component parts: (1) the water, and (2) the hardware.
\[C_{\rm cal} = C_{\rm hardware} + m_{\rm water} C_{\rm s,water} \]
The hardware heat capacity will be in units of J/K or kJ/K while the water heat capacity has to be calculated from the mass of the water and the specific heat of water (4.184 J g-1 K-1). So the water part is slightly variable due to the fact that you can fill the calorimeter up with slightly different masses of water each time you use it. If you put all that into one formula for a bomb calorimeter, you get:
\[q_{\rm cal} = C_{\rm hardware}\Delta T + m_{\rm water} C_{\rm s,water}\Delta T \]
One last thing to note. Many tables will list heat capacities using °C instead of K. Realize that these two units are equivalent in this context because we are using \(\Delta T\) and not plain \(T\). A change in Kelvin of 10 is exactly a change of 10 in °C as well. So don't try to change Celsius to Kelvin and vice versa here. This will be true throughout all your science courses.
Chemists are almost always interested in the enthalpy change to know what would have happened at constant pressure. It is possible to get \(\Delta H\) from a bomb calorimeter experiment. It just takes an additional step to do a conversion from \(\Delta U\) to \(\Delta H\).
To convert from \(\Delta U\) to \(\Delta H\) requires knowing the amount of work done (\(w\)) during the reaction. In the case of a chemical reaction, work can be easily calculated by simply counting the number of moles of gas products and gas reactants.
\[\Delta n_{\rm gases} = \Sigma n_{\rm gas\;products} - \Sigma n_{\rm gas\;reactants} \]
Now the work can be calculated with the formula:
\[{\rm work:} \hskip10pt w = -\Delta n_{\rm gases} R T \]
So this leads to the final formula for the conversion:
\[\Delta U = \Delta H - \Delta n_{\rm gases}RT \]
or with a little algebraic rearranging...
\[\Delta H = \Delta U + \Delta n_{\rm gases}RT \]
One of the key ideas of looking at state functions like the enthalpy is that the changes are the same regardless of the process taken from the initial to the final state.
This allows us to take advantage of existing data to calculate the enthalpy changes for reactions we may not have been able to perform or study. This is because even if we cannot directly measure the change in the enthalpy, we can imagine a new process which involves a number of steps that can (or have) been measured. The enthalpy change for the overall process is the sum of the enthalpy change of the steps in the process. This is known as Hess's Law and is given in the following equation.
\[\Delta H_{\rm rxn} = \Delta H_1 + \Delta H_2 + \Delta H_3 + \cdots \]
Consider the energy diagram given below. The total enthalpy for the grouping of compounds and their amounts are given and their energy differences are shown.
The overall reaction is the balanced equation for the combustion of methane.
\[\rm CH_4 (g) + 2 O_2 (g) \rightarrow CO_2 (g) + 2 H_2O (l) \]
The enthalpy for this combustion reaction is -890 kJ mol-1. However, we can imagine this reaction happens in two steps. First the methane and oxygen react to from CO(g) and H2O(l) with some oxygen left over. Next the CO and the O2 react to form CO2(g) (with the H2O already from the first step). The net reaction is the same, which means that the change in enthalpy (\(\Delta H\)) is the same. We can then see that the overall enthalpy change should be the same as the sum of the two-step process
\[\Delta H_{\rm rxn} = \Delta H_1 + \Delta H_2 = -607 + (-283) = -890 \;{\rm kJ\; mol^{-1}}\]
This is Hess's Law in the simplest case of just 2 steps giving an overall reaction. In practice there could be numerous steps to combine to get the overall reaction. You just have to keep track of the separate steps that are involved.
Often when adding up different steps for a reaction the data, we might have could be written in "the wrong direction" or have a different number of moles. However, since the enthalpy change is just the final state minus the initial state, any reaction written in the opposite order will have the same enthalpy with the opposite sign.
\[{\rm CH_4 (g) + 2 O_2 (g) \rightarrow CO_2 (g) + 2 H_2O (l)} \hskip 3em \Delta H_{\rm rxn} = -890 \;{\rm kJ\; mol^{-1}}\]
\[{\rm CO_2 (g) + 2 H_2O (l)\rightarrow CH_4 (g) + 2 O_2 (g)} \hskip 3em \Delta H_{\rm rxn} = +890 \;{\rm kJ\; mol^{-1}}\]
If you change the coefficients in the balanced equation (say by multiplying by two), then the enthalpy will change accordingly
\[{\rm 2CH_4 (g) + 4O_2 (g) \rightarrow 2CO_2 (g) + 4H_2O (l)} \Delta H_{\rm rxn} = 2(-890) = -1780 \;{\rm kJ\; mol^{-1}}\]
NOTE: Know that sometimes the "rxn" as a subscript on \(\Delta H\) is sometimes just shown as "r". So know that \(\Delta H_{\rm rxn}\) and \(\Delta H_{\rm r}\) are equivalent and both refer to the enthalpy of reaction.
The standard enthalpy of formation (\(\Delta H_{\rm f}^\circ \)) is defined as the enthalpy change for creating one mole of a compound from elements in their standard states. The standard states are the form you would find an element in at 1 bar pressure and 25 °C.
For example, the standard enthalpy of formation for CH4 would be denoted as \(\Delta H_{\rm f}^\circ ({\rm CH_4(g)})\) and would be the enthalpy change for the following reaction
\[\rm C(s,graphite) + 2H_2 (g) \rightarrow CH_4 (g)\]
Carbon is denoted as being graphite as the energy would be different for the absurd reaction run with the diamond form of carbon. Since hydrogen is a molecular gas under standard conditions, this is the form required in the standard reaction.
It is important to note that the enthalpy of formation for any element in its standard form will be exactly zero since for such a reaction the reactants (initial state) and the products (the final state) are identical and thus cannot have any change in enthalpy. For example the "reaction" for the formation of molecular oxygen gas is
\[{\rm O_2 (g) \rightarrow O_2 (g)} \Delta H = 0\]
The enthalpy of formation of a non-standard form is non-zero. Also, the enthalpy of formation will depend on the state of the compound that is being formed. For example, the enthalpy of formation of gaseous water will be higher than the enthalpy of formation of liquid water (They will be different by the enthalpy of vaporization of water, \(\Delta H_{\rm vap} \)).
Enthalpies (or heats) of formation are extremely useful in calculating reaction enthalpies. That is because any reaction can be visualized as taking place via a path in which first all the reactant compounds are converted to elements and then all the elements are converted in the product compounds. The first step in this process will be the negative of the sums of the enthalpies of formation of the reactants. Negative since it is the reverse of the formation reaction (compounds to elements). The second step is the sum of the enthalpies of formation of the products.
\[\Delta H_{\rm r}^\circ = \Sigma\,n\, \Delta H_{\rm f}^\circ {\rm (prod)} - \Sigma \,n \,\Delta H_{\rm f}^\circ {\rm (react)} \]
For more information on this important concept, please download and read Dr. McCord's Help Sheet on Standard Reactions of Formation.
Bond enthalpy (also known as bond energy) is defined as the amount of energy required to break one mole of the stated bond. For example, the bond energy of a O-H single bond is 463 kJ/mol. This means that it requires 463 kJ of energy to break one mole of O-H bonds. Note: In order to break any bond, energy must be absorbed. Therefore, bond breaking is always an endothermic change (ΔH > 0). Conversely, energy is always released upon the formation of a bond. Therefore, bond making is always an exothermic change (ΔH < 0). Find a list of bond energies in the table shown at the bottom of this page.
Change in reaction enthalpy (ΔHrxn) can be approximated from bond energy data. One can assume that during a chemical change, all bonds in the reactants are broken yielding free atoms as shown in step 1 in the diagram below. Then those atoms recombine to form the new bonds found in the products (step 2).
The overall reaction enthalpy change is easily obtained via Hess' Law:
\[\Delta H_{\rm rxn} = \Delta H_1 + \Delta H_2\]
To summarize, the change in enthalpy for a given reaction will the combined total of the energy required to break any bonds that are broken and the energy released from any bonds that are formed.
\[\Delta H_{\rm rxn} = \Sigma \Delta H_{\rm breaking} + \Sigma \Delta H_{\rm making}\]
This is the sum of the bond enthalpies of the broken bonds minus the sum of the energies of the bonds that are formed (since forming bonds will release energy). One advantage of this method is that you only need to look at the bonds that are changing in a given reaction.
Example: Consider the hydrogenation of ethene to give ethane.
\[\rm C_2 H_4 (g) + H_2 (g) \rightarrow C_2 H_6 (g)\]
Here, we need to break the C=C bond in ethene, and the H-H bond in H2. Then we need to form two new C-H bonds and a C-C bond in ethane. (See Bond Energy table at the bottom of this page) A H-H bond enthalpy (BE) is 436 kJ/mol, a C=C bond is 602 kJ/mol, a C-C bond is 346 kJ/mol, and a C-H BE is 413 kJ/mol. All of the changing energies for the reactants and products for this reaction are shown in the table below.
| reactants | ΔH | products | ΔH |
| break 1 C=C @ +602 = | +602 | make 1 C-C @ -346 = | -346 |
| break 1 H-H @ +436 = | +436 | make 2 C-H @ -413 = | -826 |
| total breaking | +1038 | total making | -1172 |
Combining both sides gives: +1038 -1172 = -134 kJ/mol
Although the above method is the most efficient in that you only break what you have to, you can also calculate the enthalpy by breaking all the reactant bonds and forming all the product bonds. This results in the change in enthalpy being the sum of the all the reactant bond enthalpies minus the sum of all the product bond enthalpies. "Bond Enthalpy" or "Bond Energy" is simply shown as BE in the formula below:
\[\Delta H_{\rm rxn} = \Sigma BE_{\rm reactants} - \Sigma BE_{\rm products}\]
This can often be a very lengthy calculation if there are a lot of bonds, so you should practice to just look and calculate for the bonds that are changing as in the example above.
In the table of bond energies shown below, please note that the top table is for single bonds and the bottom table is for double and triple bonds. Make sure you have the right bond for your specific compound(s).